Piramida regulată Aria și volumul piramidei

În această lecție vom discuta despre piramida regulată, vom vedea ce este apotema piramidei, înălțimea piramidei și vom prezenta formulele pentru aria și volumul piramidei.

Să ne reamintim! Un poligon regulat este un poligon cu toate laturile și toate unghiurile congruente (de exemplu pătratul sau triunghiul echilateral).

Piramida regulată este o piramidă cu baza poligon regulat și care are muchiile laterale congruente. În consecință, fețele laterale ale unei piramide regulate sunt triunghiuri isoscele.

Piramida patrulatera regulată este piramida cu baza pătrat și muchiile laterale congruente (fețele laterale sunt triunghiuri isoscele).

Piramida triunghiulara regulată este piramida cu baza triunghi echilateral și muchiile laterale congruente (fețele laterale sunt triunghiuri isoscele).

Tetraedrul regulat este o piramidă triunghiulară regulată având muchia laterală egală cu muchia bazei. Așadar, un tetraedru regulat are toate muchiile egale și toate fețele sunt triunghiuri echilaterale.

Apotema piramidei (notăm a_p) este înălțimea unei fețe laterale.

Înălțimea piramidei (o notăm cu h) este distanța de la vârful piramidei la planul bazei.

Aria și volumul piramidei patrulatere regulate. Aria și volumul piramidei triunghiulare regulate

Aria laterală a unei piramide este suma ariilor fețelor laterale. Aria totală a piramidei este egală cu aria laterală la care se adună aria bazei. Volumul unei piramide este o treime din produsul dintre aria bazei și înălțimea piramidei. Iată formulele pentru aria și volumul unei piramide regulate:

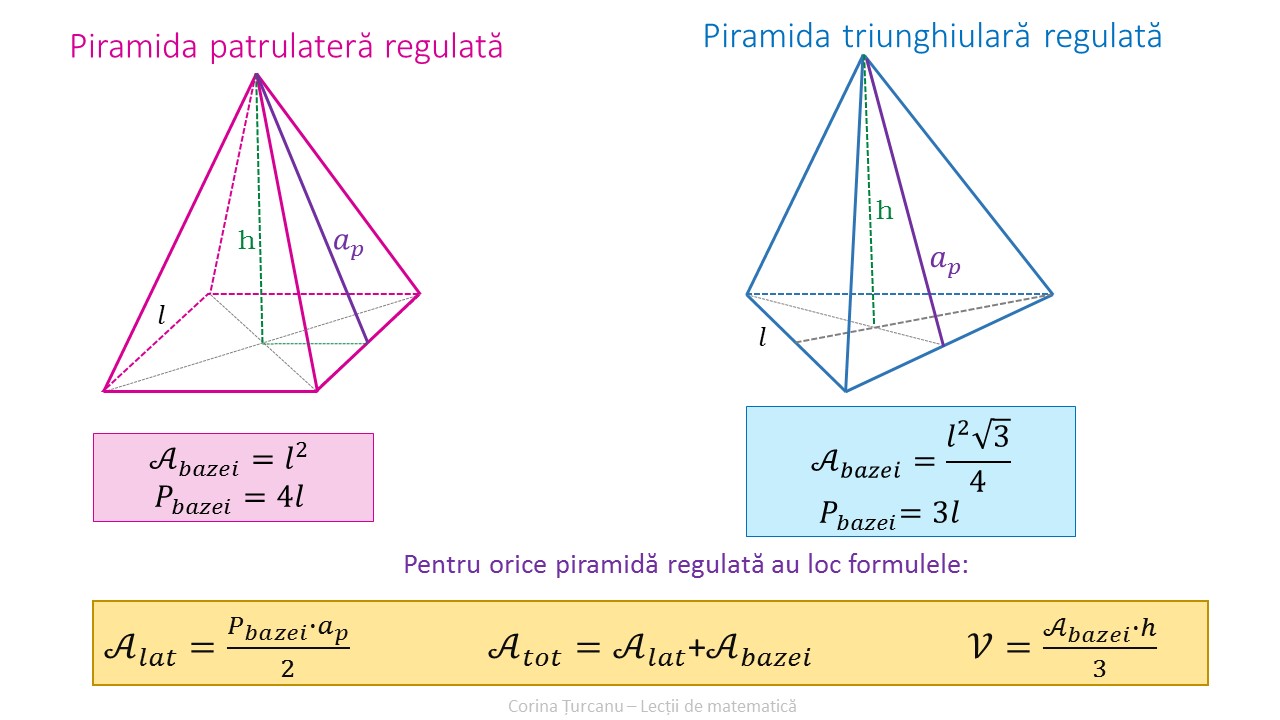
Aria totală a tetraedrului regulat se poate calcula înmulțind cu 4 aria unei fețe (triunghi echilateral).

Probleme rezolvate cu Piramida regulată Aria și volumul piramidei

Problema 1

Fie SABCD o piramidă patrulateră regulată cu baza ABCD. Dacă latura bazei are lungimea egală cu 6 cm și muchia laterală este de 9 cm, aflați aria totală și volumul piramidei.

Rezolvare:

Fie SM apotema piramidei, SM⊥BC. Triunghiul SBC este isoscel, prin urmare SM va fi și mediană, deci M este mijlocul laturii BC.