Trunchiul de piramidă regulată
În această lecție vom discuta despre trunchiul de piramidă: arie şi volum. Mai întâi vom prezenta elementele trunchiului de piramidă, apoi formulele de calcul pentru aria laterală, aria totală și volumul unui trunchi de piramidă, iar la final vom rezolva probleme cu trunchiul de piramidă.
Prin secționarea unei piramide regulate cu un plan paralel cu baza se obțin două corpuri: corpul de sus este o piramidă asemenea cu piramida inițială, iar corpul de jos se numește trunchi de piramidă regulată. În figura de mai jos avem un trunchi de piramidă patrulateră regulată și un trunchi de piramidă triunghiulară regulată.
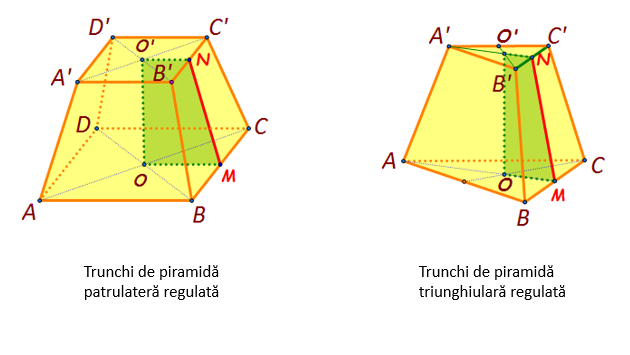
Elementele unui trunchi de piramidă patrulateră regulată:
În continuare vom scrie elementele trunchiului de piramidă patrulateră regulată:
- vârfurile: A, B, C, D, A’, B’, C’, D’
- bazele: baza mare pătratul ABCD și baza mică pătratul A’B’C’D’
- fețele laterale: trapezele isoscele ABB’A’, B’BCC’, C’CDD’, D’DAA’
- muchiile laterale: AA’=BB’=CC’=DD’
- muchiile bazei mari: AB=BC=CD=DA
- muchiile bazei mici: A’B’=B’C’=C’D’=D’A’
- înălțimea trunchiului (distanța dintre cele două baze): OO’; punctele O și O’ sunt centrele celor două baze
- apotema trunchiului (este înălțimea unei fețe laterale): MN
- apotema bazei mari: OM (M este mijlocul lui [BC])
- apotema bazei mici: O’N (N este mijlocul lui [B’C’]).
Aria laterală, aria totală și volumul trunchiului de piramidă
Pentru orice trunchi de piramidă au loc formulele:
unde: Al – aria laterală, PB – perimetrul bazei mari, Pb – perimetrul bazei mici, at – apotema trunchiului, At – aria totală, AB – aria bazei mari, Ab – aria bazei mici, V – volumul trunchiului, h – înălțimea trunchiului.
Perimetrele bazelor și ariile bazelor se calculează în funcție de poligonul de la bază.
Trunchiul de piramidă patrulateră regulată are bazele pătrate. Formulele pentru perimetrul pătratului și aria pătratului sunt:
Trunchiul de piramidă triunghiulară regulată are bazele triunghiuri echilaterale. Formulele pentru perimetrul pătratului și aria triunghiului echilateral sunt:
Probleme rezolvate cu trunchiul de piramidă
Problema 1
Fie ABCDA’B’C’D’ un trunchi de piramidă patrulateră regulată cu latura bazei mari egală cu 12 cm, latura bazei mici egală cu 4 cm și înălțimea de 8 cm. Aflați:
a) aria totală și volumul trunchiului;
b) volumul piramidei inițiale din care provine trunchiul.
Rezolvare:
OM=AB/2=12/2=6 cm
O’N=A’B’/2=4/2=2 cm
Ducem NP⊥OM ⟹OPNO’ dreptunghi ⟹OP=O’N=2 cm ⟹PM=6-2=4 cm.
În continuare vom calcula apotema trunchiului: NM, folosind teorema lui Pitagora în triunghiul dreptunghic NPM, cu NP=O’O=8 cm și PM=4 cm:
NP2+PM2 = NM2
82+42 = NM2
Am aflat apotema trunchiului și în continuare putem afla aria laterală:
Pentru a afla aria totală, trebuie să calculăm ariile bazelor. Bazele sunt pătrate, așadar:
Ab=42=16 cm2
AB=122=144 cm2
Aria totală a trunchiului de piramidă este egală cu aria laterală plus ariile bazelor:
Să calculăm acum volumul trunchiului de piramidă:
b)
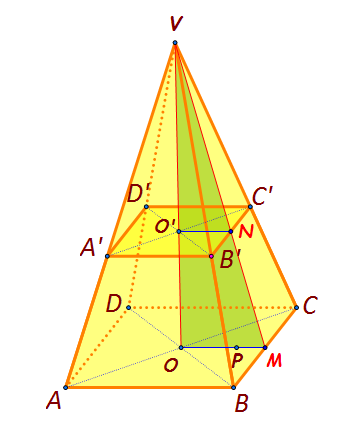
Pentru a afla volumul piramidei inițiale, trebuie să aflăm înălțimea piramidei VO.
O’N este paralela cu OM, deci triunghiurile VO’N și VOM sunt asemenea, iar laturile lor sunt proporționale:
Înălțimea piramidei este h=VO=VO’+O’O=4+8=12 cm. Volumul piramidei VABCD este:
S-ar putea să-ți placă și
Prisma regulată dreaptă
Teorema celor trei perpendiculare. Calculul distantelor în spațiu
