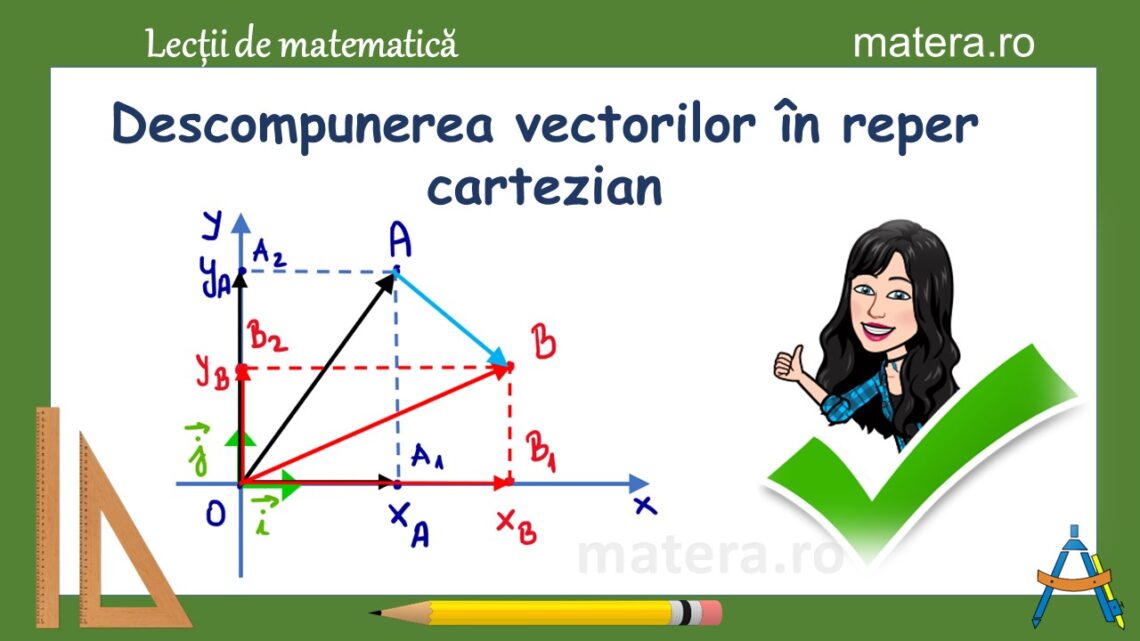
Vectori în reper cartezian

Salut! În această lecţie discutăm despre descompunerea vectorilor în reper cartezian. Considerăm reperul cartezian xOy şi notăm cu

\vec {i} \space şi \space \vec {j}

versorii axelor de coordonate (versori = vectori unitate, având modulul egal cu 1 şi direcţiile perpendiculare).

Orice vector se poate scrie cu ajutorul celor doi versori şi vom spune că am descompus vectorul după cei doi versori, astfel:

Descompunerea vectorilor în reper cartezian. Expresia analitică a unui vector

Dacă A şi B sunt puncte în sistemul cartezian, având coordonatele:

A(x_A, y_A) \space şi \space B(x_B, y_B),

atunci vectorul AB se poate scrie astfel:

\color{red}  { \vec{AB}=(x_B-x_A) \cdot \vec {i}+(y_B-y_A) \cdot \vec{j},}

formulă care poartă numele de expresie analitică a vectorului AB sau descompunerea vectorului AB după direcţiile versorilor i şi j.

Modulul unui vector

Modulul sau lungimea unui vector se poate calcula după formula:

\color{red} {|\vec{AB}|=\sqrt {(x_B-x_A)^2+(y_B-y_A)^2}. }

Operaţii cu vectori şi proprietăţi:

Fie vectorii:

\vec{u}=x_1\cdot\vec{i}+y_1\cdot\vec{j} \\ \vec{v}=x_2\cdot\vec{i}+y_2\cdot\vec{j}.

Au loc relaţiile:

1.Înmulţirea unui vector cu un scalar alfa:

\color {blue}  {\alpha \cdot \vec {u}=\alpha x_1\cdot\vec{i}+\alpha y_1\cdot\vec{j}, \alpha \in \R}

2. Adunarea vectorilor:

Adunarea vectorilor se face pe componente:

\color{blue}\vec{u}+\vec{v}=(x_1+x_2)\cdot\vec{i}+(y_1+y_2)\cdot\vec{j} 

3. Egalitatea a doi vectori:

Doi vectori sunt egali dacă coordonatele lor sunt egale:

\color{blue} \vec {u}=\vec{v} \Longleftrightarrow x_1=x_2, y_1=y_2

4. Coliniaritatea a doi vectori:

Doi vectori sunt coliniari dacă coordonatele lor sunt proporţionale:

\color{blue}\vec{u}, \vec{v} \space coliniari \Longleftrightarrow \frac{x_1}{x_2}=\frac{y_1}{y_2}

Te invit să urmăreşti lecţia video de mai jos în care am explicat formulele şi vei găsi de asemenea şi exerciţii rezolvate cu vectori.